51 replies to this topic

[alesgar]

Me equivocaré, pero el sentido comun me dice que infinitas. Claro que igual es porque no entiendo qué es medio punto xd

[DeathScythe]

Me limite a desarrallar la formula y me da -1/8, ahora ya hablando de logica pues puede ser 0 o infinitos arcos, ya me sorprenderan con la respuesta xDDDDDDDDDD

[Harlock]

He votado por la opción más popular Aunque no le veo mucho sentido. Un punto es una abstracción, una definición matemática. El concepto de "medio punto" es absurdo en si mismo. Y si lo hacemos tridimensional (corporeo), medio punto = un punto ----> 0 rectas. No lo pillo.

[Faralis]

Yo pensaba que zero ... peeeero estas no son horas que mañana curro ... ya me contareis ....

[Bloodberry]

Primero, yo di las mates básicas y eso no lo di, pero bueno, de todos modos falta la opción no lo sé, no me hace falta criticar la pregunta o a quien lo hizo.

[Juslibol Lord]

llevo una castaña del copón, mañana curro, infinito suena bien, alacascala

[Loele]

al menos en geometria basica no existe "medio punto" el punto es la unidad minima e indivisible y como dijiste matematicas basicas no es ni infinito ni cero sino "no aplica" xd la ultima opcion digamos

[shavart]

Como aquí cada uno sale por donde le apetece yo también.

¿Cómo pasamos un punto a un continuo? Bueno, pues digamos que ese elemento de dimensión 0 le añadimos una dimensión por la cara.Si antes estaba (por ejemplo) en un espacio de dimensión dos y sus cordenadas eran (x,y), ahora será (x,y,t) con "x" e "y" fijas y "t" variable. Esa recta sería un punto, medio punto vendría a ser la mitad de los elementos de ese subespacio de dimensión 1.

Por mantener que 2 "puntos" se pueden unir con un solo arco, eso arcos de antes ahora serían superficies que contienen a los "puntos". La mitad de una superficie seguirá siendo una superficie, no tiene que ver con la consideración de antes con el punto. Entonces según cómo tomemos la media recta tendremos infinitas superficies para unir esos nuevos puntos (si elegimos un conjunto discontinuo) o en el caso de que fuera un conjunto continuo la única superficie que se me ocurre sería una degenerada que fuera la propia media recta.

Así que dependería de si la media recta te la hace un tío dando un hachazo, 50 hachazos o un matemático dando n hachazos. xD
Y yo... me voy a acostar que es tarde.

[obi]

Puta mierda de la funcion gamma... Ale, me toca repasar.

[Takamura]

Bueno, al principio pensé que sería una pregunta con trampa y que tendría algo que ver con un arco de medio punto de la arquitectura.

¿Me ha quedado cava de nochevieja y voy efectivamente ciego? ¿Estoy dando pistas falsas? ¿Me habré confiado? ¿He tomado como básico algo que se resuelve con splines? Cuántas dudas...

Es que en tu problema faltan datos. Los datos que das no determinan de forma única la fórmula que tienes en la cabeza. Anoche estuve pensando que sería algo del palo de la función gamma de Euler, igual que obi, aunque en la función gamma ya partes de una fórmula para los números enteros y buscas una función que cumpla otras propiedades aparte de interpolar los valores enteros, como cumplir (x+1)! = x! * x, ser infinitamente derivable, etc.

Por ejemplo, el problema de la gallina... pues la mayoría de la gente daría esa respuesta (o no), pero un matemático probablemente te diría que no tiene sentido, que faltan datos o que hay infinitas respuestas, y un ecólogo te daría una respuesta completamente distinta, porque la cantidad de huevos que ponga una población de gallinas no varía de forma lineal con su número en un hábitat de recursos limitados, eso solo se da en condiciones especiales de granja, cuando a las gallinas las alimentan aparte a cada una, y no se tienen en cuenta los efectos de los cambios de temperatura, etc.

Me acuerdo de un libro de matemáticas (Conceptos de matemática moderna, Ian Stewart) donde ponían un problema de calcular el mínimo de una función (era el logaritmo de algo, no me acuerdo exactamente). Uno se ponía a derivar la función, miraba dónde se anulaba la derivada, calculaba la derivada segunda y demostraba que era un mínimo. Voila. Luego le pedían el valor del mínimo y cuando lo iba a calcular... obtenía log(0), que no está definido. El autor usaba este problema como ejemplo de que la matemática no es manejar fórmulas. Cuando vi tu problema me vino a la mente este.

[Vaughamm]

Voy a responder antes de que se acumule más resentimiento contra mí xD

La clave es centrarse en el problema. De nada sirve intentar averiguar qué es medio punto o un número no entero de arcos puesto que ya dije que no tenía sentido, así que eso hay que dejarlo a un lado.

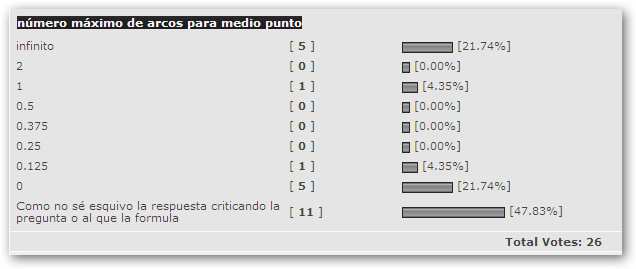
En el caso concreto el número máximo de arcos va así:

0 puntos:
No tenemos un punto de origen así que no podemos trazar ningún arco

Pintamos 1 punto
Tenemos un punto de origen pero no uno de destino, así que tampoco ningún arco

Pintamos otro punto más: 2 puntos
Del punto inicial pintamos un arco al nuevo

...

Pintamos otro punto más: n puntos
De cada uno de los anteriores podemos pintar un arco al nuevo punto: x_n = x_(n-1) + n -1 o la suma desde 0 hasta n-1 o x_n = n*(n-1)/2

De esto nada importa teniendo la última fórmula excepto una cosa: esto es el máximo número de arcos. Por ejemplo, si tenemos 5 puntos podemos pintar 0,1,2.... ó 10 arcos, siendo 10 el máximo.



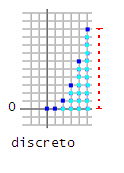
Ese número máximo crece según una parábola o polinomio de 2º grado. Ahora si pasamos a contínuo los puntos y arcos pierden todo el sentido pero igualmente llamamos al eje x puntos y al eje y arcos y conservamos el planteamiento.

(Si se quiere ver como interpolación f(x) = x*(x-1)/2 interpola mejor que cualquier otra fórmula a la discreta n*(n-1)/2 y es infinitamente derivable, continua, sin mala leche ni cosas chungas. No veo por qué habría que buscar otra cosa distinta.)

Para un número real de puntos x tenemos un intervalo real de valores posibles en y, lo que llamamos arcos.



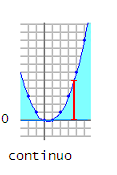
Dicho intervalo de valores posibles está en el área que delimita la función. Y de hecho no hay que hacer ningún cálculo. Sólo hay que saber hacia dónde mira la parábola, cuyo coeficiente para el cuadrado es positivo. Sabemos que para 0 y para 1 corta el eje x, luego entre medias los valores son negativos. Y el máximo entre un número negativo y cero es cero.



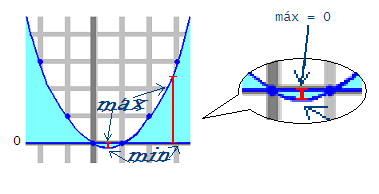
Lo del valor absoluto lo puse para no duplicar opciones en la encuesta. En todo caso -0.125 sería el mínimo. 0.125 sería el máximo del valor absoluto, no el valor absoluto del máximo. pero si no queremos admitir un número de arcos negativos seguiría siendo cero el máximo.

Como veis la fórmula es correcta y el problema es básico, tan básico como saber la pinta de una parábola y qué el máximo es el número mayor de todos.

Afortunadamente es un sumatorio y no un multiplicatorio, porque entonces aparecería Euler nos daría por culo a todos, porque eso o lo manejas habitualmente u olvidas la gamma, la beta y todo el alfabeto griego.

Г(½) = √π

Edited by Vaughamm, 04 January 2008 - 02:27 PM.

[Zeatanas]

¿esto es matematica basica?

Vamos, dudo que ningun niño de la ESO salga sin conocer algo asi...


P.D.- Manda cojones.

[marengo]

0 puntos:
No tenemos un punto de origen así que no podemos trazar ningún arco
Pintamos 1 punto
Tenemos un punto de origen pero no uno de destino, así que tampoco ningún arco

Pos si con un punto de origen y 0 de destino no alcanza para hacer un arco, con medio punto de origen y 0 de destino ...

Pintamos otro punto más: n puntos
De cada uno de los anteriores podemos pintar un arco al nuevo punto: x_n = x_(n-1) + n -1 o la suma desde 0 hasta n-1 o x_n = n*(n-1)/2

¿Cómo se demuestra eso? Por inducción. Pero si vamos al caso continuo, la inducción ya no vale. Te entiendo lo de que medio punto es una forma de hablar, pero así mismo tampoco tiene sentido usar la fórmula en el caso continuo porque queda bonica xD. No sé, 0 arcos lo entiendo, puede estar mal o bien, pero 1/8 de arco negativo no lo pillo.

[Vaughamm]

Interesante:

¿esto es matematica basica?

Vamos, dudo que ningun niño de la ESO salga sin conocer algo asi...


P.D.- Manda cojones.

Es el planteamiento el que no es básico

Edited by Vaughamm, 04 January 2008 - 02:44 PM.

[Harlock]

Ya me imaginaba que la respuesta iría por ahí, pero estoy con marengo... esto no es una cuestion basica... ni matematica, sino una apreciacion puramente subjetiva. Sin acritud, pero esto es mas un chiste que un problema

[obi]

Pintamos 1 punto
Tenemos un punto de origen pero no uno de destino, así que tampoco ningún arco

Estoy en contra de esta suposición, para un solo punto tienemos infinitos arcos, dadas las propiedades del espacio de Minkowski en el que vivimos, tambien se puede afirmar lo mismo aplicando algunas propiedades del espacio de euler...

Las matematicas no son absolutamente ciertas nosotros somos los que le damos la logica, bajo tu suposición tu solución es correcta, pero como es necesario hacer esa suposición, no la has dado en el enunciado y hay otras posibilidades esta pregunta de examen queda invalidada.

Spoiler

Sin acritud, mi primer pensamiento fue el de Vaughamm pero pense que tenia que tener trampa y me puse a jugar con la funcion gamma...

[Takamura]

Si te pareció que iba con mala idea, te garantizo que no, pero sigo pensando que el problema está mal planteado. Un chiste de matemáticos que creo que viene a cuento para esto:

Van en un tren un matemático, un físico y un ingeniero. Están viajando por Irlanda, cada uno de camino a un congreso. Miran por la ventanilla y ven una oveja negra en medio de un prado. Dice el ingeniero:
— Vaya, las ovejas de Irlanda son negras.
Y le corrige el físico:
— No, en Irlanda algunas ovejas son negras.
Y dice el matemático:
— En Irlanda hay al menos un prado, donde hay al menos una oveja, uno de cuyos lados, al menos, es negro.

[azurhialine]

Hombre, la aplicación de la fórmula de esa forma (como ya me imagino que al plantear el acertijo habrás tenido en cuenta - ya has dicho que no tiene sentido) es lo que haría el típico que se la suda por completo lo que le preguntan y se limita a aplicar fórmulas, no se si me explico.

Vamos, que es como si yo te digo que necesitas poner 28,45 pilotes en una losa para cimentarla. Muy bonito, precioso, lo clavo, pero demuestro que no tengo ni zorra de lo que es un pilote, lo que es la ingeniería ni lo que es la vida real y el sentido común.

Me suena a lo de "podo mellon e minno" o algo así, que venía en las puertas de Moria. Una solución tan obvia que hasta al más docto de los hombres no se le ocurriría aplicarla.

Dicho de otro modo. Daba igual si hablábamos de arcos y nodos (o puntos) que hablar de bocas y penes. La cosa al final era pasar de la raíz del problema (que en principio consistiría en definir lo que es un medio punto, o si no es posible tal cosa) e ir a la fórmula, al modelo creado, supuestamente, para simular una realidad.

Este topic refleja, en cierto modo, errores que se cometen (y que todo el que ha manejado números de cierto nivel ha cometido) en ingeniería, ciencias y otras ramas, que es el de abstraerse tanto en la solución matemática que te olvidas de la solución técnica. O sea, el ir tanto a la fórmula y al número que no te das cuenta que lo que estás planteando no es viable. No será al primero que le pasa, en mi trabajo, que, hace un modelo en 3D de una estructura, monísimo, con sus nudos, barras, fuerzas, condiciones de contorno... vamos, una filigrana, y se encuentra que salen unas tensiones increíbles, del cagarse. Y dice, "bah, pues armamos hasta el culo y solucionado". Claro, luego ves el modelo y te das cuenta que estás planteando un mecanismo, o cuasi-mecanismo* que hace que la estructura no trabaje como tu te planteabas. Y peta.

*Se define como mecanismo en estructuras cuando una estructura no es, como mínimo, isostática (existen estructuras hiperestáticas), es decir, no cumple la ecuación de (Nº condiciones de apoyo) + (Nº barras) >= 2*(Nº de Nudos). O sea, dicho en vulgo, tiene elementos "moviles". Normalmente no se plantea un modelo estructural de mecanismo, sino que se plantean modelos "críticos". O sea, que están a punto de ser un mecanismo por la disposición de las barras y nudos en ellos y la posible existencia de barras que no son capaces de absorber los esfuerzos recibidos.


O sea, que el problema tiene solución matemática válida, aunque luego no tenga una solución geométrica clara (o no la tenga en absoluto, aunque por si acaso lo digo con la boca no muy grande).

Edited by azurhialine, 04 January 2008 - 03:40 PM.

[Frikjan]

PD: Lo que puso Frikjan de integrales y de lo que se arrepintió después me gustó. Ya las "veréis" cuando lo explique

Es que luego vi lo de "Básicas" y me dije que no podía ir por ahí la cosa, aunque tampoco me parece que la forma fuera correcta creo

[Vaughamm]

Estoy en contra de esta suposición, para un solo punto tienemos infinitos arcos, dadas las propiedades del espacio de Minkowski en el que vivimos, tambien se puede afirmar lo mismo aplicando algunas propiedades del espacio de euler...

Las matematicas no son absolutamente ciertas nosotros somos los que le damos la logica, bajo tu suposición tu solución es correcta, pero como es necesario hacer esa suposición, no la has dado en el enunciado y hay otras posibilidades esta pregunta de examen queda invalidada.

Si tenemos dos puntos podemos como máximo trazar una línea o arco entre ellos.

Si con un punto tenemos infinitos arcos entonces el máximo para dos puntos no sería uno. El indicar que el máximo para dos puntos es un arco y no infinitos (y 3 para 3, 6 para 4...) hace que esa suposición esté implícita. No se invalida nada salvo que tengas una posibilidad distinta coherente con el enunciado (y que incluya el no usar matemáticas avanzadas, cosa que también está en el enunciado)

[jaierf]

Lluege tarde para la polemica pero como casi la mayoria "Critico al que hizo el planteamiento"
Cuando uno entra y mira el poll diciendo "numero maximo de arcos para medio punto" lo primero que se le ocurre es que el man esta loco.
Ademas, que eso es basico??
Quizas lo tenga pero me dejo como loco fue lo de los arcos y medio punto, tocaria ver desde otro punto de vista y saber como se puede interpretar eso.
Con este hilo el señor en cuestion nos muestra que todo las respuestas estan bajo nuestra nariz y no las vemos..